UM UNIVERSO DE 10 DIMENSÕES Quanto mais longe mais INCRÍVEL TUDO FICA

 A existência de dimensões extras é explicada usando o coletor Calabi-Yau, no qual todas as propriedades intrínsecas das partículas elementares estão escondidas. Crédito: A Hanson.

Em matemática, as variedades de Calabi-Yau são variedades complexas análogas, de maior dimensão, às superfícies K3. Algumas vezes elas são definidas como variedades de Kähler compactas cujo fibrado canônico é trivial, embora muitas outras definições parecidas mas não equivalentes também sejam usadas de vez em quando. Elas foram chamadas de espaços de Calabi–Yau,  em homenagem a Eugenio Calabi, que estudou tais variedades, e a S. T. Yau, que provou a conjectura de Calabi de que este tipo de variedades têm métricas Ricci flat

Este tipo de variedade apresenta-se, por exemplo, no contexto da geometria algébrica, e também em física teórica. Particularmente na teoria das supercordas, as dimensões extras do espaço-tempo são algumas vezes conjecturadas a tomar forma de uma variedade de Calabi–Yau de dimensão 6, levando à ideia de simetria especular.

Uma variedade de Calabi-Yau é uma variedade de Kähler compacta com uma primera classe de Chern nula. O matemático Eugenio Calabi supôs em 1957 que tais variedades admitem uma métrica Ricci-flat (uma em cada classe de Kähler), e essa conjectura foi provada por Shing-Tung Yau em 1977. Consequentemente, uma variedade de Calabi-Yau pode também ser definida como uma variedade Ricci-flat de Kähler compacta.

É também possível definir uma variedade de Calabi-Yau como variedade com uma holonomia SU(n). Outra condição equivalente é que a variedade admita uma (n, 0)-forma holomórfica global nunca nula.
 Além dessas três dimensões visíveis, os cientistas acreditam que pode haver muitos mais. De fato, o arcabouço teórico da Teoria das Supercordas postula que o universo existe em dez dimensões diferentes. Estes diferentes aspectos são o que governa o universo, as forças fundamentais da natureza e todas as partículas elementares contidas.

A primeira dimensão, como já foi observado, é aquilo que lhe dá o comprimento (também conhecido como o eixo dos x). Uma boa descrição de um objeto unidimensional é uma linha reta, que existe apenas em termos de comprimento e não tem outras qualidades discerníveis. Adicione a ele uma segunda dimensão, o eixo y (ou altura), e você obtém um objeto que se torna uma forma bidimensional (como um quadrado).

A terceira dimensão envolve profundidade (o eixo z), e dá a todos os objetos uma sensação de área e uma seção transversal. O exemplo perfeito disso é um cubo, que existe em três dimensões e tem um comprimento, largura, profundidade e, portanto, volume. Além destas três, são as sete dimensões que não são imediatamente evidentes para nós, mas que ainda podem ser percebidas como tendo um efeito direto sobre o universo e a realidade tal como a conhecemos.

A linha do tempo do universo, começando pelo Big Bang. De acordo com  a Teoria das Cordas, este é apenas um dos muitos mundos possíveis.

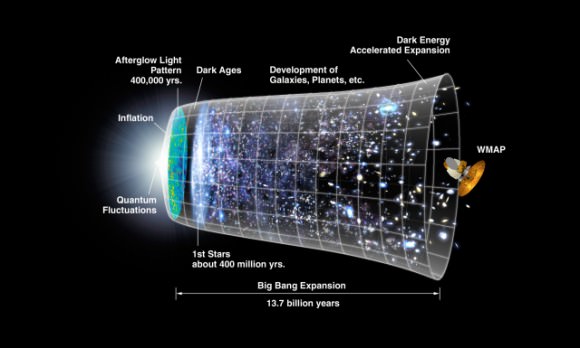A linha do tempo do universo, começando pelo Big Bang. De acordo com a Teoria das Cordas, este é apenas um dos muitos mundos possíveis. Crédito: NASA

Os cientistas acreditam que a quarta dimensão é o tempo, que rege as propriedades de todas as questões conhecidas em qualquer ponto. Junto com as outras três dimensões, conhecer uma posição de objetos no tempo é essencial para traçar sua posição no universo. As outras dimensões são onde as possibilidades mais profundas entram em jogo, e explicam sua interação com os outros é onde as coisas ficam especialmente complicadas para os físicos.

De acordo com a Teoria da Supercorda, a quinta e a sexta dimensão são onde a noção de possíveis mundos surge. Se pudéssemos ver até a quinta dimensão, veríamos um mundo um pouco diferente do nosso, que nos daria um meio de medir a semelhança e as diferenças entre nosso mundo e outros possíveis.

Na sexta, veríamos um plano de mundos possíveis, onde poderíamos comparar e posicionar todos os universos possíveis que começam com as mesmas condições iniciais que este (ou seja, o Big Bang). Em teoria, se você pudesse dominar a quinta e sexta dimensão, você poderia viajar de volta no tempo ou ir para futuros diferentes.

Na sétima dimensão, você tem acesso aos mundos impossíveis que começam com diferentes condições iniciais. Enquanto na quinto e sexta,as condições iniciais eram as mesmas e as ações subseqüentes eram diferentes, aqui, tudo é diferente do início dos tempos. A oitava dimensão novamente nos dá um plano de histórias de universo tão bizarras, cada uma das quais começa com diferentes condições iniciais e se ramifica infinitamente (daí por que elas são chamadas de infinitos).E tudo que é infinito é meio incrompreensível.

Na nona dimensão, podemos comparar todas as histórias possíveis do universo, começando com todas as diferentes leis possíveis de física e condições iniciais. Na décima e última dimensão, chegamos ao ponto em que tudo o que é possível e imaginável é coberto. Além disso, nada pode ser imaginado pelos humildes mortais, o que torna a limitação natural do que podemos conceber em termos de dimensões.

O espaço em Corda - a teoria das superconjuntos vive em 10 dimensões, o que significa que seis das dimensões devem ser "compactificadas" para explicar por que só podemos perceber quatro. A melhor maneira de fazer isso é usar uma geometria 6D complicada chamada
 coletor Calabi-Yau, no qual todas as propriedades intrínsecas das partículas elementares estão escondidas. A teoria dos superconjuntos vive em 10 dimensões, o que significa que seis das dimensões devem ser "compactificadas" para explicar por que só podemos perceber quatro. A melhor maneira de fazer isso é usar uma geometria 6D complicada chamada um coletor Calabi-Yau, no qual todas as propriedades intrínsecas das partículas elementares estão escondidas.